かけ算に順序なんてあるの?
2018-03-01
追記2019.12.5
かけ算の順序を問題視している人たちは、小学校での算数の指導方法を知らないようなので、書いておきます。※自分がピカピカの小学一年生だった時を思い出して読んでいただけると、懐かしいと思います。
まず一年生のはじめに数の数えかたを習います。
カブトムシの足の数は何本か?を数える時は、一本の足ずつ数えます。
これでカブトムシの足の数の数え方を理解します。このやり方では、3匹のカブトムシの足の数を数えるのに、最初は1本ずつ18回数えることになります。
これでも足の数は出せるのですが、いちいち数えるのはめんどくさいので、足し算という新しい概念を教えます。
カブトムシの足の数は6本+6本+6本と、ひとかたまりを1単位として3回足すことを教えます。
次に、かけ算という新しい概念を教えます。
カブトムシの足の数は6本をひとかたまりとして3つ分で表せることを教えます。
つまり、6本x3つ分という新しい概念です。
こういう流れでかけ算の概念を教えたのち、九九を丸暗記させます。
ここで重要なのは、一つ分の数(かけられる数)と いくつ分(かける数)がどっちがどっちかを理解させることです。
3匹のカメがいます。カメの足はそれぞれ4本です。足の数は何本ですか?という問いが出た場合、文章通りの数で書くと、
3x4 となります。3x4は、(かけ算には交換法則があるため)数学的には正しいのですが、小学校では、一つ分の数(かけられる数)X いくつ分(かける数)と書かせることによって、ひとつ分(かけられる数)がどっちなのかを理解しているか?をチェックする必要があるため、4x3とかかせます。
逆に書いた子に対しては本人に確認することになります。
3匹のカメがいます。足の数は全部で何本?の場合、3×4と、そのまま書く子供は、いくつ分がどっちなのか?を理解してない可能性があります。
こういったケースでは個別にきちんと確認して教えます。
(確認やフォローの仕方は下記の本ブログ参照)この時、かけられる数とかける数をきちんと理解した上で逆に書いてる場合があります。
その時は、「こんな事でバツをつけられて点数が下がるのはもったいないから、かけられる数×かける数 の順番に書いてね。
そしたら先生もいちいちチェックせずに楽だから。」と説明します。ほとんどの子は納得してそれ以降間違いません。
なぜなら、本当にかけ算の概念を理解しているし、先生の言うことが理解できたからです。稀に、かけられる数とかける数がどっちかを理解しているのに教師への嫌がらせでわざと逆に書く子もいます。
そういう子には再度説明するのですが、それでも教師に対する嫌がらせ行為を繰り返すようなら、内申点に協調性がない。とか、教師の言うことを聞けない子。と書かれちゃいます。普通の親は、先生の言うことはきちんと聞きましょう。と指導していると思うので、子供は先生の意見に従います。
従えない子は、算数はできても社会性のない子、もしくは日本語の読解力のない子という認識になります。学校は、知能の高い子も低い子も同列に対処しないといけないため、いちいち嫌がらせをする子に構ってられないのです。
そんなことよりは本当に理解できていない子に教師は注力するのです。
小学校は「数学」を学ぶところではなく、日本で生活をするうえでの基本的な知識と共用と、協調性、団体行動を学ぶところなのです。
追記2019.12.9
あすなろ199 かけられる数×かける数
ここに、簡潔に、論理的に、数学的にも納得のいく回答がありましたので記載させていただきます。
追記2019.10.21
かけ算の順序の件に関して、色々言ってくる人がいますので、私の見解を先に述べておきます。今回のかけ算の順序問題で、「かけ算の順序が間違っていたらバツをつけるのはおかしい!」といっている人が勘違いしている点がいくつかあるのが理解できた。
一つ目は、「順序が間違っていても答えがあっていれば△にしかならない」のにバツになると考えている点。
つづく— いいな (@iina_kobe) October 20, 2019
二つ目は、順序が間違っていて部分点しかもらえなかった場合、そこで子供が放置されて、「子供が意味がわからずに算数が嫌いになる!」と考えている点。実際には個人個人にフォローが入るので、放置はされない。
つづく— いいな (@iina_kobe) October 20, 2019
三つ目は式の順序が間違っていても◯をつけた場合、一つ分の数がどれで、いくつ分なのかがどれなのか?という日本語をそもそも理解できていない子供を救ってあげれないという事を理解していない点。
義務教育なので、日本で暮らせる最低限の日本語を理解させるのが目的なのを、学習塾と間違えている。— いいな (@iina_kobe) October 20, 2019
四つ目は、長方形の面積を求める問題などで、 一辺×一辺 の場合は順序はどうなるの!といっている点。単位が同じなら、どっちでもいい。
ただし、縦かける横の順番で書きなさい。と指定されている場合は、その通りに書かないとバツとなる。答えがあってれば、答えは◯。— いいな (@iina_kobe) October 20, 2019
五つ目はかけ算を教える過程で、一つ分のかたまりが何個分 と、生徒がわかりやすいように便宜的に順番に書いているだけなのに、中学の数学になっても大人になってもかけ算に順序があるなんておかしい!と言っている点。
かけ算には順序はありません。し、交換法則も教えるので、子供は混乱しません。— いいな (@iina_kobe) October 21, 2019
この5点に関して全部理解していて、かつ、議論したいなら、むしろ私は大歓迎です。
単なる煽りとかは時間の無駄なので、やめて欲しいですね。
— いいな (@iina_kobe) October 21, 2019
かけ算に順序なんてあるの?
っていう話題がまたぶり返しているようです。
私も2013年11月22日に、
掛け算に順序なんてあるの?
というタイトルのメルマガを書いておりましたので、かけ算の順序問題について、このブログにも書き残しておきたいと思います。
Contents
解答がXになった例
今回の事の発端は、このツイートでした。
とうとう遭遇した pic.twitter.com/kNvRmZEku3
— ケイタ (@fmty) February 26, 2018
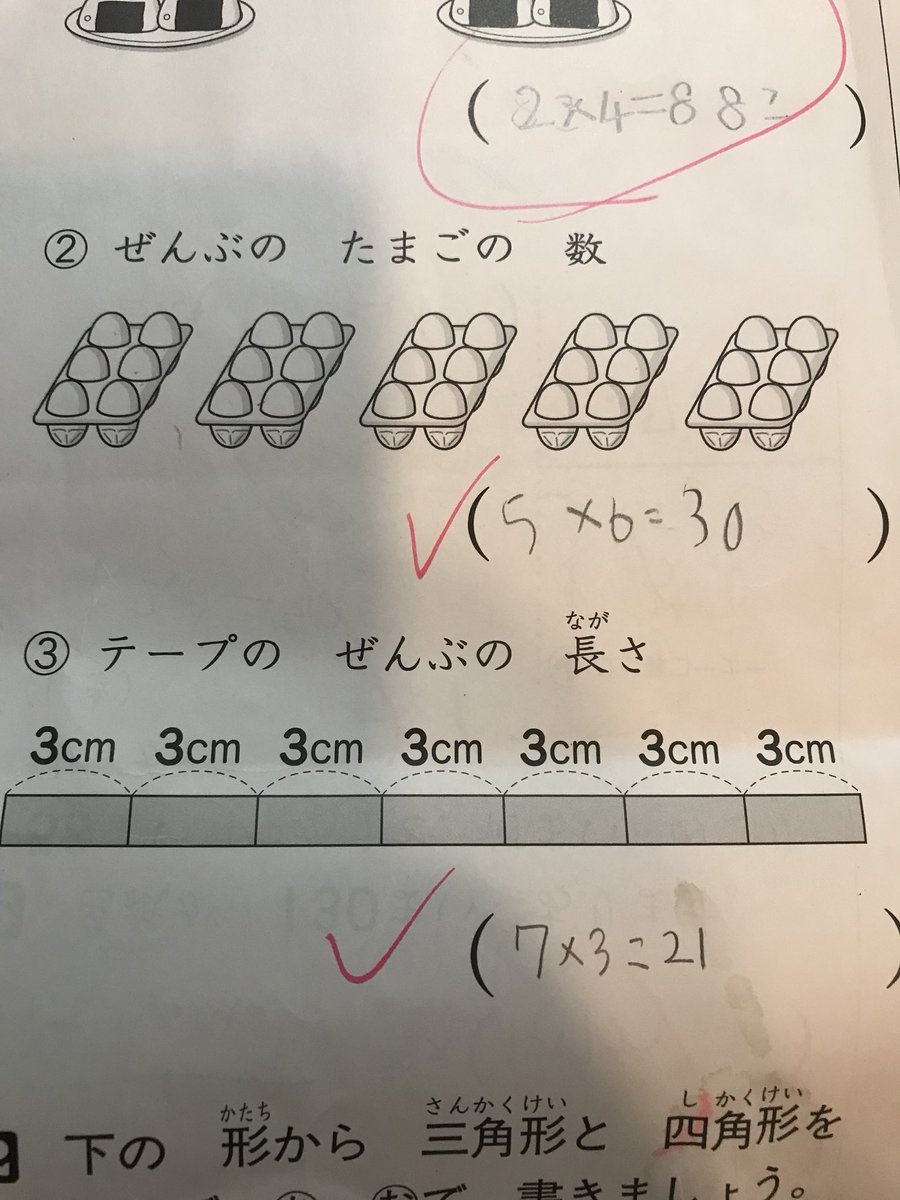
この図の通り、
6個が1パックになったタマゴが5パック、計30個あります。
この卵の個数を計算するのに、
5x6=30
5(パック)x6(個)=30(個)として答えを出したら、不正解となった。ということです。
さらに、
3センチのテープが7つ続いたテープの長さを求める際に、
7x3=21
7(本)x3(センチ)=21(センチ)として答えを出したら、不正解となった。ということです。
普通の社会人なら、
どっちも正解やろ?
って思うと思います。
しかし、
「小学校の最初に習う算数のかけ算では、一つしか正解ではないんですね。」
掛け算に順序なんてあるの?
そんなの常識的におかしいだろ!っていう人のために、メルマガ「生物学博士いいなのぶっちゃけていいっすか?」のno.29「掛け算に順序なんてあるの?」(2013年11月22日発行)から、一部抜粋してみます。
以下メルマガよりコピペ
↓
発端のブログ
掛け算に順序があるのかないのか?っていうのが話題となっていますので、ちょっと整理してみます。
発端はこのブログです。
6×8は正解でも8×6はバッテン?あるいは算数のガラパゴス性
引用します。
★僕にも解けない算数の問題
僕はブログにはプロジェクトワーク以外のことは書かないことにしていたのだが、あまりに憤慨したのでちょっと聞いて欲しい。
写真は、娘(2年生)の算数のテスト。

8人にペンをあげます。1人に6本ずつあげるには、ぜんぶで何本いるでしょうか。
ご覧のように、「8×6」だとバッテンで、「6×8」だと正解らしい。
何じゃこりゃ。
僕がテストを受けたとしても「8×6」と書く。
だって問題文はその順番に書いてあるから。
さらに答の48本もバツ。丁寧に赤ペンで48本と直してくれている。
さらに意味不明。
★娘にヒアリングしてみた
「何でバッテンだったか、先生説明してくれた?」
「単位が違うと、式の順番が違うんだって」
「? 意味分かる?」
「全然分かんない」
「じゃあ・・ウサギには2本の耳がある。ウサギは4羽いる。耳は全部で何本?」
「ずつ、が入ってないからどっちが先か分かんない。答えは8本だけど」
「じゃあ・・ウサギには2本ずつ耳がある、だったら?」
「それなら、2×4=8本」
「ずつ」がある方を先に書く、と覚えている訳です。
うーむ、教育上じつによろしくない状況ですな。
★かけ算では書く順番が大事??
不思議に思って「かけ算 順序」などでWebを検索してみたところ、状況が見えてきた。
・どうやら今の小学校では、かけ算の記述順にこだわりがあるらしい
・こだわりの順序とは逆に書くと、×にする教師が多い
・当然ながらそれについては論争があり、×にすることに対してナンセンスという意見もある。
赤ペン先生で有名なベネッセが「かけ算の順番が逆だったらバツにすべきだよ派」らしいので紹介したい。
かけ算の式は「一つ分の数」×「いくつ分」の順に書く約束になっているので、問題文から正しく読み取って、その通りに式をかけるようにしましょう。
小学校では、式の意味を理解することが大切なので、このような約束があります。
どうやら、
「6×8」と書くと「6本×8人」を意味するのだが、
「8×6」と書くと「8本×6人」を意味することになってしまうのでNG
ということらしい。
僕はこれを読んで益々考え込んでしまった。そもそもこんな約束あったっけ?
わり算だったら、書く順番は大事だ。でも、かけ算にはどうでもよくね?
日々かけ算を使っている僕ら大人が知らなくても困らない「約束」って、存在意味があるのだろうか?
そしてこの「約束」に従って採点することは、数学的にどうなんだろうか??
(以下略)
大切なお約束
はい、引用ここまで。
この人は、
小学校で、一番最初に掛け算を教える時の基本的なお約束である、
かけ算の式は「一つ分の数」×「いくつ分」の順に書く約束になっているので、問題文から正しく読み取って、その通りに式をかけるようにしましょう。
小学校では、式の意味を理解することが大切なので、このような約束があります。
を理解していませんね。
小学校二年生で掛け算を習う最初、ほぼすべての子供が、
かけられる数(一つのかたまりにある数)x かける数(いくつぶん)
と習います。
ただし、世界共通ではありません。
国の言語の文法によって違うみたいです。
日本語での算数のかけ算
ここからは、日本のおはなしだと思ってみてくださいね。
8人にペンをあげます。1人に6本ずつあげるには、ぜんぶで何本いるでしょうか。
という文章題では、上のお約束に従い、
「一つ分の数」(かけられる数)が6本で、「いくつ分」(かける数)が8人ぶんですので、
6x8が正解です。
かけ算は、足し算の後に習います。
ここが重要。
かけ算は、足し算の延長上にあるのです。
この問題の場合、足し算でいうと、6本+6本+6本+6本+6本+6本+6本+6本=48本となります。
9人になったら、6本(一つのかたまりにある数)が、1人分増えるので、6本を足しましょう。
でも、6x9のほうが簡単だよね!
っていう教え方をします。
なので、8x6だと、8人のかたまりが6本分=48人となってしまうのです。
足し算でいうと、8人+8人+8人+8人+8人+8人=48人となります。
9人になったら、9人(一つのかたまりにある数)が、1本分増えるので、8を足しましょう。
となっちゃいます。
日本語的におかしいですよね。
なので、8x6だと「文章題の式としては」バツなのです。
しかし、このブログ主の娘さんのテストでは、答えが「48本」でバツになってますね。
これは、先生がおかしいです。
この場合、式がバツ、答えは正解のはずです。
しかもこの先生、式がバツなのはなぜ?
という問いに対して、きちんと教えていない模様です。
普通の先生なら、上に書いたように、
きちんとかける数とかけられる数の概念を教え、「乗法(掛け算)のやり方」を説明し、子供に、あっ!そうか!と納得させるのです。
しかし、この先生はそれをやっていない。
これに対して怒るのは、親としてごもっともです。
日本の教育指導要領に基づいた指導法
乗法のやり方の指導法は、
かけ算の式は「一つ分の数」×「いくつ分」の順に書く約束になっている
ので、これに従わないと少なくとも、日本でかけ算を習った直後ではバツになります。
このブログの筆者がそれを習っていないというのであれば、それはブログ主の先生にも問題があったのでしょう。
戦後の義務教育では、一貫して、かける数とかけられる数の概念は教えているはずです。
この、「かける数とかけられる数の概念」が、
「教育指導要領にのっていない!」
もしくは、
「教育指導要領には掛け算の順番なんか書いてない!」
と怒る人がたくさんいます。
はたしてそうでしょうか。
教育指導要領の解説には、
・「乗法が用いられる場合とその意味」
乗法は、一つ分の大きさが決まっているときに、その幾つ分かに当たる大きさを求める場合に用いられる。
つまり、同じ数を何回も加える加法、すなわち累加の簡潔な表現として乗法による表現が用いられることになる。
とかかれてます。
つまり、
足し算でもいいけども、その「延長線上の表現に」掛け算があるんだよ。
ということです。
上の例でいうならば、
6本(一つのかたまりにある数)が、1人分増えるので、6を足しましょう。
の部分ですね。
そして、
・乗法に関して乗数が1増えれば積は被乗数分だけ増えるという性質や、
乗法についての交換法則について児童が自ら調べるように指導する。
と明記されています。
「乗法に関して乗数が1増えれば積は被乗数分だけ増えるという性質」つまり、
8人にペンをあげます。1人に6本ずつあげるには、ぜんぶで48本いります。一人増えたらあと何本いるでしょうか。
という問題があった時、
6(被乗数、かけられる数)x8(乗数、かける数)+6(被乗数分)=54本
と、
6(被乗数、かけられる数)x9(=8+1、乗数、かける数)=54本
という性質を理解させましょう。
また、
この場合、9人x6本でも同じ「数」になりますね。という交換法則を児童が見つけるように指導しましょう。
ということなのです。
交換法則を用いる前の大前提
なので、交換法則を使用できるのは、「かける数」と「かけられる数」がどっちがどっちなのか?を理解していることが大前提となります。
そして、この、「かける数」と「かけられる数」がどっちがどっちなのか?を理解しているかどうか?
を試すために、
8人にペンをあげます。1人に6本ずつあげるには、ぜんぶで何本いりますか?
という、数字的には先に8、後に6が出てくるので、8x6と書きたいひっかけ問題をだしてチェックするのです。
そして、8x6と書いて間違った場合には、もう一度、
乗法に関して乗数が1増えれば積は被乗数分だけ増えるという性質
を説明し、生徒に納得してもらうのです。
ようは、どっちが「かけられる数」で、どっちが「かける数」なのか、を理解してもらうのです。
これが二年生での指導法です。
4年生になっても、この「文章題のひっかけ問題」は出てきます。
そして、間違う子供もたくさんいます。
そして、先生は、「思い出してごらん?かけられる数とかける数を習ったでしょう?」
と問います。
すると、生徒は、「あっ!そうか!」と思い出すわけです。
これは、教師歴40年の先生に聞いたので、間違いないです。
かけ算自体には順序はないが、文章題の場合には順序がある
ということで、何故、掛け算に順序なんてあるの?
なんていう「題」になったのか、わからないんですが、しいて言うなら、
掛け算には順序なんてありません。
しかし、「文章題の場合には」、「かけられる数」と「かける数」が定義されていて、
「乗法に関して乗数が1増えれば積は被乗数分だけ増えるという性質」
を利用してこの問題を解きなさい!というのが問いなわけですから、
そのルールに則って、式を書き、答えを書く。
のが基本となります。
このルールを知らない、もしくは守れない親が、モンスターペアレンツとかになってしまうわけです。
このルールができた理由
このルールがどうやってできてきたのか?に関しては、
昔からこの方法で理解度の確認作業をやってきて問題なかったから
としか言いようがないです。
かけ算で、なんで「はっぱろくじゅうし」っていうの?
っていうのと同じで、それで覚えたほうが速いから。
としか言いようがありません。
もっとも、これ以外にもっといい方法があるよ!っていうんであれば、その方法で教科書を書けばいいと思います。
それが効率的ならば、その教科書を使う学校が増えるでしょう。
学校はルールを守る力をつける場所
学校教育法
第二十一条 義務教育として行われる普通教育は、教育基本法 (平成十八年法律第百二十号)第五条第二項 に規定する目的を実現するため、次に掲げる目標を達成するよう行われるものとする。一 学校内外における社会的活動を促進し、自主、自律及び協同の精神、規範意識、公正な判断力並びに公共の精神に基づき主体的に社会の形成に参画し、その発展に寄与する態度を養うこと。
(以下略)
とありますように、
学校教育は、社会的活動、集団行動を通して、規範意識や判断力を養うためにあります。
定められたルールに従って、立式し、問題を解くのがルールであって、このルールに従って乗法などを理解する工程が出来上がっているわけです。
足し算の後に掛け算を習うのは、この工程を踏んでいくからなのです。
先に掛け算を習う人は違う工程を踏むことになります。
学校では、ルールに従わないならば、バツになります。
これは大人の世界でもそうです。
交換法則を使って数を扱えるようになるのは、あくまでも、
「乗法に関して乗数が1増えれば積は被乗数分だけ増えるという性質」
を理解したうえでのことです。
そして、この基礎となる性質を理解しているならば、ひっかけ問題で間違うなんてことはありません。
間違うならば、それは、理解できてないって事なのです。
算数は、数学とは違います。
算数は、国語の要素も含んでいるんです。
数学のように単なる数字を扱うのではなく、日本におけるリアルな生活を元にした数字の取り扱い方を教えるのが算数です。
要は、「かけ算の順序問題」は、数学で言う数字だけの問題なのでなく、もっと大きい意味での「物事の考え方の問題」「日本語の問題」なわけです。
かけ算は、足し算という基礎の延長上にある「応用」です。
足し算を理解してから、かけ算を応用によって理解するのです。
小学生の時の一つ一つの積み重ねの「考え方」という基礎を理解させず、「楽な方」を教えちゃうと、基礎が育たない。
だから、これを「おかしい!」と問題視する人は、他人に基礎を教える能力がないということになる。自分が理解しているからわかるだろ!ってのは、ただの上から目線でしかない。— いいな (@iina_kobe) February 28, 2018
小学校では、「かける数とかけられる数」を明確に分けて「頭の中で想像しやすい形にして、思考能力を養うのが目的」であり、これを、算数といっています。「答えの数値を出す」のが目的の「数学」とは全くの別物。算数には、国語力も入ってきます。算数の文章題とかは国語力も必要です。
— いいな (@iina_kobe) February 28, 2018
順序や単位は理解度の確認のために要求される
2018.11.18追記
毎年恒例の、この時期に盛り上がる「かけ算に順序なんてあるの?」問題ですが、今年もまたまたクソリプ質問がたくさん来ました。
みなさん、まだまだ納得されていないようなので、今回のやり取りで私自身が気付いたことをまとめておきます。
まず、義務教育とは、すべての子供に一定レベルの知識をつけさせることを基本としております。
ですので、生徒一人一人に対し、きちんと把握できているのか?を確認する作業を一番大事にします。
いや、ですから義務教育では、あぶり出して、どんな子にもわかるように指導しますよ。そのための、理解してるかどうかを確認するための順序ですから。
それ以外の確認方法があればそれをすりゃいいと思いますけどね。 https://t.co/rJeu3PpP6S— いいな (@iina_kobe) November 17, 2018
知恵袋に、このような質問と回答がありました。
kam********さん 2011/3/1016:22:57
Q:算数の文章題を解く時、式に単位は必要ですか?
小学校で算数の問題を解く時、式に単位を書かないと、遠い昔に習った気がするのですが・・・
子どものテストで式に単位を書かなかった為、×になりました。(計算も答えも正解でした)
式に単位が必ず必要な時はありますか?
(略)wat********さん 2011/3/1016:45:48
A:式に単位は不要です。
式というのは、数量の関係を表すものですから、単位があろうとなかろうと成立することを想定していますので。ただし、初等教育(小学校など)では、単位が一致しない、もしくは不適切な立式をする事が初学者の場合多いため、注意を喚起する意味で「式にも単位をつけてちゃんと確認しなさい」と指導している例が多いように思います。
確かに、立式をして変な状態だったときに、単位(次元)を確認したら両辺で単位(次元)が違っていたなんていうこともあったりしますので、わかりやすくはあります。
では、単位は必ずつけなくてはいけないか?という事ですが。必ずしもつける必要はありません。
確かに、等式を作る際に、両辺の単位(次元)が一致していなくてはいけませんが、その確認さえきちんとできれば、式変形をするときなどはむしろ邪魔ですね。面倒臭くなるだけです。
ですから、通常の場合であれば「式に単位をつけることは普通はしない」ということになります。そこで、今回の対応ですが。 「式にも単位をつけること」を指導されている先生の元で試験を受ける場合にだけ、ローカルルールと思って単位をつけて解答するのが無難ですね。
ただし、あくまでローカルルールですので、学年があがってもっといろいろなケースで学習するようになれば、自然にグローバルルールが身に着くと思います。
(略)
まさに、
初等教育(小学校など)では、単位が一致しない、もしくは不適切な立式をする事が初学者の場合多いため、注意を喚起する意味で「式にも単位をつけてちゃんと確認しなさい」と指導している例が多い
ですね。
かけ算の順序の問題も同じです。
不適切な立式をする事が初学者の場合多いため、注意を喚起する意味で「かけられる数とかける数の順番をつけて、ちゃんと確認しなさい」と指導しているのです。
要するに、理解度のチェックのためにやっているわけです。
(りんごが三個ずつ4つの皿の上に載っています。りんごの数は全部でいくつでしょう?という問いの場合)
生徒がそう回答してきた場合、うちの親は「かけられる数とかける数を思い出してごらん?」というそうです。「あっ!そうか」と3×4に直す子は理解してると判断。「かける数×かけられる数の順番でもいいよね?」とか言ってくる子にはみんながわかるようにかけられる数×かける数の順番で書いてね。と指導 https://t.co/8zF9L5eg3p
— いいな (@iina_kobe) November 17, 2018
問題分に4が先に出てきたから4×3と書いた子はそもそもかけられる数とかける数を理解してないから居残りで教える。と、その子の能力に応じた対応をしてます。
しかしながら、今の教師はそれすらできていないと嘆いとります。 https://t.co/8zF9L5eg3p— いいな (@iina_kobe) November 17, 2018
公立の義務教育は、きちんと把握しているか?の確認作業が1番大事なのよね。高校とか大学の、やりたいやつだけついて来ればいい。ってスタンスとは違う。全員がある一定の基準を超える事を目標としているんだから、物足りない子は塾に行くなり好きにすりゃいいのよ。ただ、邪魔はしないでほしい。
— いいな (@iina_kobe) November 17, 2018
実際の現場の声
2018.11.24追記
実際、塾などではどう教えているのか?っていうのを聞きましたのでまとめておきます。
順一さんは福島県で塾をしております。
おはようございます。
僕のところでは、掛け算の順番に関しては例えば「3つのリンゴが入った袋が5つあります。全部で幾つのリンゴがありますか。」という問題なら、問題の文脈を理解させる様に説明した上で3×5の順番で書くように指導してます。— 順一 (@jyunichidesita) November 18, 2018
ただ、生徒の子どものタイプによって、そこでバツにしてしまう事でマイナスに働きそうだなと判断出来た場合はマルをあげた上で「〜っていう理由で、掛け算も順序を気にして式を立てた方が良いんだよ。」と説明して以降注意する様に促す、といった感じで指導してます。
— 順一 (@jyunichidesita) November 18, 2018
テストの場合、公平な採点となると思うのですが、その場合、式に5×3と書いたらバツとなりますか?
— いいな (@iina_kobe) November 18, 2018
例えば塾独自のテストで採点するのであれば、僕の場合は周辺の学校の採点方針に合わせています。例えば近隣の小学校でバツにされてるのであれば塾においてもバツにして、学校でバツを貰わない様に指導してあげるべきかと思います。
— 順一 (@jyunichidesita) November 18, 2018
もちろん、なぜその順番で書くべきなのかの説明はした上でですが、なかなか納得出来ない子もいるのも事実ですね。
— 順一 (@jyunichidesita) November 18, 2018
ありがとうございます。最後に、かけ算の順序でバツをもらった子供のことで、親が出てきて学校や塾ににクレームをつけてきた場合は、その親に対しても説明しますか?
説明した場合、親がそれを納得しないケースはありますか?— いいな (@iina_kobe) November 18, 2018
僕は父兄から文句を言われた経験は無いですが、もしそういう事があればきちんと説明して納得してもらう様に努力すると思います。小学校教育は問題を解くだけでなく、問題を解く上で必要な思考経路を構築する事が大事だという事を分かって貰いたいですね。
— 順一 (@jyunichidesita) November 18, 2018
というわけで、やはり、塾では、子供のことを考えた教育をなさってらっしゃるようです。
神戸で塾をしている方にもお聞きしました。
かけ算の順序について、大学生や塾の講師の方とお話してきました。結論から言うと、自分が今なにをしているのか?がわかっているのかを確認する国語力の問題なので、逆に書くとバツにする。とのこと。また、全国統一テストなどでも、逆に書くと部分点となるらしいです。なので、ブログ通りでした。
— いいな (@iina_kobe) November 18, 2018
問題に書かれている数字が「個」なのか、「km」なのか「kg」なのかを文章から読み取れない子供は、高校の問題で意味が読み取れずに苦労するという事例がたくさんあるとの事なので、小学校のうちに、その数字がなんの数字なのかを理解させておくことが大事であるとの事でした。
— いいな (@iina_kobe) November 18, 2018
どうやら、全国統一テストでも、順序を逆に書くと部分点となるようです。
やはり、「きちんと理解できているかどうか?」を問う問題では、順序が重要なようですね。
中国人留学生にも聞いてきました。
あと、中国人留学生にもかけ算の順序について聞いてきました。中国では、かけ算の順序は「理解してるなら」どっちでもいいらしいです。が、学校の教師のやる事にクレームをつける子供や親は呼び出され、きちんと説明をするとの事。それでも理解しない子供は他校に転校させられるとの事。
— いいな (@iina_kobe) November 18, 2018
中国の場合、小学生は主に「遊ぶことや友達を作ること」に重点を置いているため、小学生で塾に行かせることは少ないようです。
そして、「かけ算の順序はどっちでもいい」そうです。
ただし、クラス単位での平均点とかをものすごく気にするようで、理解していないのに〇となった場合、もう少し難易度の高い文章題が解けなくなる可能性があるので、そういう子は後でいろいろと大変となるようです。
また、先生の立場が非常に強いようで、親が教師の教えに背いたりクレームを言うことはめったにないとのことです。
もし、親がクレームなどを学校に入れた場合は、校長や教師、その親やそのクラスの親などを呼んで、きちんと話し合いを持つそうです。
そして、その子供と教師がうまくいかないと判断された場合は、クラス全体のことを考えて、その子を違う学校に転校させるということでした。
中国では、個よりも集団を大事にしているみたいですね。
大学生にも聞いてきました。
学生の数学がめっちゃできる子1人は、大学受験の二次試験において、式の数字を意味もなく逆に書いたりした場合も部分点となる可能性があると言ってました。
また、彼は算数は苦手らしく、算数と数学は全く別物だと言ってました。やはり、算数には国語を理解する力が必要であるとの事です。— いいな (@iina_kobe) November 18, 2018
彼が言うには、大学の二次試験などでは、必要がないのに数字の順番を入れ替えると部分点になる場合があるということでした。
それは数字の単位などを理解していないから。ということでした。
彼は、「算数は国語力も必要なので、算数は今でも得意ではない」と言ってました。
しかし、数式は大好きらしく、○○の定理を解いてるんです。とか、私には理解できないことを言ってました。







コメント
物理屋
2年で交換法則の説明として「1行あたり5個の3行分」も「1列あたり3個の5列分」も同じ物だということを習うにもかかわらず、文章題で順序が逆だと「1個あたり3行の5個分」であるかのような扱いを受けるのが腑に落ちません。兎が4羽いたら耳の数は右耳4本左耳4本の合わせて8本ではないんですか。
「ずつの付いている方が先」あるいは「答えと単位が同じ方が先」というルールがあると習っている人達が沢山います。これは、”意味を考えずに順序だけ約束通りにするため”のテクニックが広まったものです。あなたも書いているように、バツなのは何故という問いに対してきちんと教えることをやっておらず、ルールだけ守らせています。発端のブログもそうです。元々の由来がどうであれ、この状況で保護者に対して「意味を理解することが大切なので約束を守らせる」と言っても説得力がありません。この方法で問題が無かったのは、もはや過去の話です。
一つ分の数・幾つ分は教えているはずですが、順序が全国で一貫して教えられてきたわけではありません。手段は各々の学校に委ねられています。指導要領に累加の簡潔な表現として用いられるとは書いてありますが、一つ分の大きさが先で幾つ分が後でなければならないとまでは書いていません。順序が定められているという解釈について、文科省は「深く考えすぎだと思う」と言っていたそうです。
本筋からは外れますが、本来「掛けられる数・掛ける数」とは単に「×の前に書かれている数・後に書かれている数」のことを指します。掛け算順序は、掛けられる数を先に書く指導ではなく、一つ分の数を掛けられる数にする指導です。
数学の目的が「答えの数値を出す」というのは大きな誤解です。証明問題に代表されるように、算数以上に思考能力が重要で、文を組み立てる力も必要です。「ソクラテスは人だ。そして、人とは死ぬものだ。」が算数だとすれば「人は動物だ。そして、動物とは~」とより大きな括りについて考えるのが数学です。数字や四則演算が人、定数・変数や関数が動物に相当します。ソクラテスと人の繋がりは理解できている前提で、ソクラテスのような個々のリアルなケースに直接は触れないのが誤解の元でしょうね。しかし、科学や経済などの複雑な数字の取り扱いには算数では力不足です。
iina-kobe
コメントありがとうございます。
現状、教科書はほとんどがこのブログで書いたような表現方法を使用してます。学校では沢山の子供に教えないといけないため、学校で習うやり方通りにしないとバツになります。
最近の学校の先生は、かなり質が落ちていまして、きちんと教えるためのスキルを有してません。
これは沢山の熟練の先生達が嘆いています。
だからこそ、家庭や塾などでの教育が必要となってきております。そして、学校以外の教育を受けれない子供達との格差がどんどん開いていっております。もうこれは時代の流れなので仕方ないのです。
数学と算数は違う。というのは、小学校レベルの話です。強いて言うなら、単位のある文章問題と数値だけのかけ算の違い。という意味です。
物理屋
私が通っていた公文式もそうですが、家庭や塾は必ずしも教科書に書いてある学校で習うやり方を教えるわけではありません。そんな中、きちんと教えるスキルも無く、手が回らないのでやり方が違うとバツでは、不満の声があがるのもまた仕方ないことでしょう。「習っていない漢字を使ってはいけない」という指導も同じように問題になっていますね。
小学校レベルの話で数学を持ち出すのは、ちょっと意味が分かりません。(助数詞ではなく)単位のある問題なら、厳密にはm×m=㎡やm/秒×秒=mのような文字式が必要になるところを、場面毎に公式を用意し、数値だけ取り出して計算させるのが算数です。
iina-kobe
義務教育では、すべての人に公平に教えることが大事です。先に進んでいる人は、「順序なんかどうでもよい」と考えてしまうんですが、それを初めて習う人にとっては、順序は大事なのです。また、賢い子供は、「学校では順序が違うとXになる」ことを知っているので、きちんと正解を出せます。中途半端に知ったかぶりしてる子と、本当に理解していない子が、ひっかけ問題に引っかかるわけです。そして、義務教育では、きちんと理解しているかどうかを確認する必要があるため、こういう問題を高学年になっても出します。これは、戦後、ず~っとこうです。
小学生レベルの話で数学を持ち出したのは、「算数は読解力を身につけ、かつ、ルールに従って答えを導き出すという教育指導方針である。」ことを理解せず(理解できず?)、順序なんてどっちでもいいじゃないか!という人が多数おられたからです。
物理屋
得手不得手もありますが、「学校ではバツ」というのは案外理解しがたいものです。先に進むこと以上に。また、理解できても納得できない人もいます。
答えが単位と同じ方を先に書くと教えられたり、右耳4本左耳4本とも考えられると教えられたり、アレイ図に置き換えれば良いと教えられたりする子がいる一方で、一つ分の数の概念をきちんと教えられない先生がいるのに、順序のルールだけ確認することに何の意味があるでしょうか。順序が大事である理由がなおざりにされ、手段が目的化しています。
高学年は初めて習う人ではありませんよね。なぜ補助輪を外させないのでしょう。
iina-kobe
ブログ、ちゃんと読んでもらえばわかると思います。
凡田夏之介
交換法則を使用すれば(かけられる数)×(かける数)=(かける数)×(かけられる数)なのだから、「かける数」と「かけられる数」を理解する必要はなくなるのでは?
「交換法則を用いる前の大前提」というのは何を根拠に出てきた説なのでしょうか?
iina-kobe
ブログにも書いてますが、普通に小学校の足し算、引き算の続きとして出てくるのが大前提となってます。
凡田夏之介
論理に飛躍がありすぎて理解できません。
なぜ足し算、引き算の続きに出てくると「交換法則を用いる前の大前提」が成り立つのでしょうか?
iina-kobe
それはブログに書いてあるので、読んでみてください。
凡田夏之介
読んでもわからないのでお尋ねしています。
具体的にはどの部分に書いてあるのですか?
iina-kobe
抽出すると、以下の文章などです。
↓
かけ算は、足し算の後に習います。
ここが重要。
かけ算は、足し算の延長上にあるのです。
この問題の場合、足し算でいうと、6本+6本+6本+6本+6本+6本+6本+6本=48本となります。
9人になったら、6本(一つのかたまりにある数)が、1人分増えるので、6本を足しましょう。
でも、6x9のほうが簡単だよね!
っていう教え方をします。
凡田夏之介
抽出されている部分は分配法則に関係していても交換法則について何も言っていないのでは?
それにこれのどこから「交換法則を用いる前の大前提」が出てくるのですか?
まったく論理的なつながりが無いのですが。
iina-kobe
私のブログは、ある程度の日本語理解力と読解力を有している人用に書かれております。
「大切なお約束」と、「日本の教育指導要領に基づいた指導法」と、「交換法則を用いる前の大前提」を読んでも、なお理解できないというのであれば、私のブログはあなたのお役には立てないですし、私にはあなたの疑問を解消する能力はありません。
すいません。
なお、これ以上、「ブログを理解せずに質問」されても質問に答えることはできません。
こちらをお読みすることをお勧めします。
Twitterには「文字は分かるが文は読めない」という人が一定数存在する話
凡田夏之介
iina-kobeさんはご自身の言説を論理的に説明できないからといって、それを他人の読解力のせいにされるのですか?
確かにiina-kobeさんに能力がないことは同意いたしますが、だからといって安易に他人のせいなどにせずに、ご自身でおっしゃったことぐらいご自身で証明する程度の努力をされたらどうでしょう。
iina-kobe
私自身の言説ではなく、文科省がこういうふうに指導しなさいよ!と学校の先生に指導し、学校の先生がその通りに小学生に教えているというものですので、不満があるのでしたら文科省へどうぞ。
これだけ説明しても理解し得ないのであれば、私にできることは何もありません。
凡田夏之介
また人のせいにされるのですか?
しかも今度は嘘までついて。
文科省は乗法九九から「乗法についての交換法則について児童が自ら調べるように指導する」を言っていますが、「交換法則を使う前の大前提」を言っているのはiina-kobeさんですよ?
iina-kobe
ブログ読めば、私がなぜ「交換法則を使う前の大前提」と言っているのかわかると思ったのですが、どうやら理解されていないようなので、ブログから該当箇所を引用しておきますね。
これでもわからないのであれば、私の手には負えないので、小学校なりで先生に聞いてきてください。
たくさんのコメントありがとうございました。
以下引用
↓
ここが重要。
かけ算は、足し算の延長上にあるのです。
この問題の場合、足し算でいうと、6本+6本+6本+6本+6本+6本+6本+6本=48本となります。
9人になったら、6本(一つのかたまりにある数)が、1人分増えるので、6本を足しましょう。
でも、6x9のほうが簡単だよね!
っていう教え方をします。
なので、8x6だと、8人のかたまりが6本分=48人となってしまうのです。
足し算でいうと、8人+8人+8人+8人+8人+8人=48人となります。
9人になったら、9人(一つのかたまりにある数)が、1本分増えるので、8を足しましょう。
となっちゃいます。
しかし、このブログ主の娘さんのテストでは、答えが「48本」でバツになってますね。
これは、先生がおかしいです。
この場合、式がバツ、答えは正解のはずです。
しかもこの先生、式がバツなのはなぜ?
という問いに対して、きちんと教えていない模様です。
普通の先生なら、上に書いたように、
しかし、この先生はそれをやっていない。
これに対して怒るのは、親としてごもっともです。
日本の教育指導要領に基づいた指導法
乗法のやり方の指導法は、
ので、これに従わないと少なくとも、日本でかけ算を習った直後ではバツになります。
このブログの筆者がそれを習っていないというのであれば、それはブログ主の先生にも問題があったのでしょう。
戦後の義務教育では、一貫して、かける数とかけられる数の概念は教えているはずです。
この、「かける数とかけられる数の概念」が、
「教育指導要領にのっていない!」
もしくは、
「教育指導要領には掛け算の順番なんか書いてない!」
と怒る人がたくさんいます。
はたしてそうでしょうか。
教育指導要領には、
とかかれてます。
つまり、
ということです。
上の例でいうならば、
6本(一つのかたまりにある数)が、1人分増えるので、6を足しましょう。
の部分ですね。
そして、
と明記されています。
「乗法に関して乗数が1増えれば積は被乗数分だけ増えるという性質」つまり、
という問題があった時、
という性質を理解させましょう。
また、
ということなのです。
凡田夏之介
今度は小学校の先生に責任転嫁ですか?
何度も言っていますが「交換法則を用いる前の大前提」を言い出したのはiina-kobeさんですよ?
そして単に本文をコピペしても情報量は1bitも増えません。
何も言っていないのと同じです。
そもそも自然科学の法則の適用可否が属人的な能力によって決まるというオカルトな概念に何も疑問をもたれないんでしょうか?
iina-kobe
このお話はそもそも、「初めてかけ算を習う小学生への「日本での」教え方の話」なのです。
「算数」の教え方の話であり、「数学の話ではない」のですよ。
ブログでもコメントでも散々書いてますが、「交換法則を用いる前の大前提」は、小学生が初めてかけ算を習う前に、かけ算とはどういうものなのか?を理解するため大前提としての、「単位のある形で、かける数とかけられる数の概念を学ぶこと」という意味なんですよ。
これを理解した後に、「交換法則を習う。」ということなのですよ。
あなたがどこの国の人かは知りませんが、少なくとも日本ではこうなのです。
誰も自然科学の法則とか、オカルトとかの話はしておりません。
これすら理解できないのであれば、知識量の差がありすぎてお話になりません。
そもそもブログ読んでないですよね?
今後、わけのわからないコメントはスパム扱いとさせていただきますのでご了承ください。
t.m
はじめまして。「かけ算の順番」の検索でたどり着き、読ませていただきました。
「掛け算には順序なんてありません。」とのことですが、昨年6月に文科省がPDFを公開し、今年3月に書籍として出版された『小学校学習指導要領(平成29年告示)解説 算数編』では、「被乗数と乗数の順序が,この場面の表現において本質的な役割を果たしていることに注意が必要である。」というのが入っているほか、「被乗数と乗数の順序」と交換法則の扱いについても別に1つの段落になっていまして、結局のところ、「順序はある」と読めます。
あと「乗法に関して乗数が1増えれば積は被乗数分だけ増える性質」についてですが、交換法則との関連は薄く(「乗法に関して成り立つ簡単な性質」という程度の共通点です)、「8人にペンをあげます。1人に6本ずつあげるには、ぜんぶで何本いるでしょうか。」に対して使うには苦しいと、読んで感じました。ペンの文章題では、「かけられる数(一つ分の数)は6〔本〕」と「かける数(いくつ分)は8〔人〕」というのが、かけ算の学習においては暗黙の了解になっています。これは国内に限った話ではなく、Greer (1992)で最初の例として書かれた場面でも同様です。
「8x6だと(略)8人+8人+8人+8人+8人+8人=48人」についても、Vergnaud (1988)に同様の解釈があります(日本では、先生がそう解釈できてしまうから間違いと言うのに対して、その文献では子どもたちの気づきとなっていますが)。「日本」「日本語」を明示したのは、おそらく知的誠実さによるものと思われますが、ことさらに強調(限定)するものでもないように思っています。
iina-kobe
数学のかけ算に関しては順序はありません。しかし、「教育段階での算数」ではかけ算に順序をつけることによって、学生が理解しやすいようにして教える。ということです。
実際に理解してしまえば順序はありません。
daniyama
私も、逆でもかまわないだろうと思っていました。
が、ご説明を読んで、よくわかりました。
かけ算に順序はないが、文章題の場合には順序がある。
これは、文章題の場合、数字には意味が込められるからですよね。
大変わかりやすい説明をありがとうございました。
余所見するお味噌汁
>かけ算の式は、「一つ分の数」×「いくつ分」の順に書く約束
などという単なるローカルルールに過ぎないものを、普遍的な法則と区別せずに採点の対象とすることが問題なのです。
実際には6本のかたまりを8人分(6+6+6+6+6+6+6+6)を8×6と表記しても何もおかしくはないにも関わらず、
「8×6だと、8人のかたまりが6本分=48人となってしまうのです。」
などと、たかがローカルルールを、あたかも大前提(普遍的な真理)であるかのように扱うことが問題なのです。
これは非常に有害です。全くの嘘・でたらめを教えているのと同じことです。
「リアルな生活」には、「いくつ分」×「一つ分の数」の表記(請求書やレシートにおける「個数×単価」など)も普通に存在し、何もおかしくはありません。
にも拘わらず、このような表記が誤りであると信じて疑わない人が多くいます。
このような思い込みを刷り込んでしまう時点で、掛け算にあたかも「正しい順番」があるかのように教える教育は有害なのです。
このような思い込みは、例えば下記の発言小町のトピ主のように問題を起こします。
http://komachi.yomiuri.co.jp/t/2004/0607/002209.htm
「日本におけるリアルな生活を元にした数字の取り扱い方を教えるのが算数」であるならば、なおのこと問題でしょう。
「ルール」が「いくつ分」×「一つ分の数」となる世界も「リアルな生活」には存在するにも関わらず、
誤った「思い込み」を刷り込むことで、上記のような「ルール」に対する順応力を明らかに損なっているわけです。
これは「規範意識や判断力を養う」という観点からも明らかにマイナスであると言えるでしょう。
今まで「問題なかった」と思っているならば、それは単に問題を認識する能力がなかっただけ、ということです。
余所見するお味噌汁
>国の言語の文法によって違うみたいです。
まずこれが大嘘です。
なぜこんな出鱈目を信じる人が存在するのか不思議でなりません。
例えば、英国であってもBBCの算数教育サイトのように「一つ分の数」×「いくつ分」で統一されているところもあるようです。
フランスでは、どちらを採用するかは教師によって異なるようです。
結局のところ、言語の文法と掛け算の順序との間には全く関係が無いと言ってよく、「一つ分の数」×「いくつ分」に統一することには、何ら正当性も根拠もありません。
また、言語の文法というなら、例えば「5人に3個ずつパンを配る」という日本語は不自然ですか?
この文章から「5×3」という式を作ることは不自然ですか?
交換法則を習っているか否かなど全く関係ありません。
交換法則を考慮するまでもなく、先入観無しで見れば、上記のような立式はごく自然なものです。
且つ、上記のような立式を誤りとする根拠は何もありません(下らないローカルルール以外には)。
交換法則云々ではなく、「交換するまでもなく最初から成立する」のです。
上記のような立式が「不自然」「誤り」と見えるならば、それは「思い込み」のなせる業です。
そのような「思い込み」こそ有害であり、故に私は、特定の掛け算順序を誤りと教えるのは一刻も早く止めるべきであると考えます。
「どちらでもよい」ことは「どちらでもよい」と教えなければいけません。
「どちらでもよい」のに片方を誤りと教えるのは嘘を教えることであり許されません。
「算数の文章問題に限っては嘘じゃないよ」なんて言い訳にもなりません。
余所見するお味噌汁
次に、よくある「理解度のチェックのためにやっている」とかいう主張についてですが、
Wikipediaの「かけ算の順序問題」において触れられている通りです。
以下引用です
『かけ算の順序で「読み取り」が正しくできているかあるいは「文章題の意味を理解しているか」を判定するという考え方は不合理である。 伊藤宏の報告[18]のように絵を描かせた場合、絵を見ることによって児童が正しく問題文を読み取っているか判断できる。その結果、小学3年生において、順序の読み取りが適切にできていても問題に登場した順に書く児童のほうが多いし、「正しい順序」でない式を書いた児童でも適切に読み取りができていることが報告されている。』
あ、これ原文ママですけど誤記がありますね。文脈から分かるとは思いますが、(誤)「順序の読み取り」→(正)「問題文の読み取り」
既に説明しましたように掛け算の順序は「どちらでもよい」が正解ですから、おかしな思い込みに囚われていない子供にとっては問題に登場した順に書くことが自然なのでしょう。
『また、一旦、絵にもとづいて式と答えを書くことができるようになった児童が、かけ算の順序を指導された後、文章題が解けないと言い出し、式を書くのを躊躇するようになった例が報告されている[19]。』
ともあるように、マイナス面も無視できないようです。
もし絵を描かせるよりも簡易的に理解度を測りたいのであれば、求められる回答に無関係な情報(ノイズ)を問題文に混ぜればいいだけの話です。
例えば「3個のリンゴと4個のミカンとが入った袋が6袋あります。リンゴは全部でいくつありますか」といったように。
ノイズとなる情報を増やせば、運任せで正解する可能性をより低くし、より正確に理解度を測ることができるでしょう。
さらに、「一袋に入れるリンゴの数を4個にした場合、リンゴの数は幾つになりますか」や「袋の数を一つ減らした場合、リンゴの数は幾つになりますか」といった問いを追加してもいいでしょう。
いずれにせよ、奇妙なローカルルールを強要する必然性なんか、これっぽっちもありません。
逆に、掛け算の順序を強要することで、いかなる理解を測れるのかが、はっきり申し上げまして不明です。
(掛け算の順序をローカルルールとは逆に書いた子供が具体的に何を理解していないことになるのか、及び、それを理解していない場合には具体的にどんな問題が発生するのか、が不明ということです。)
「式の順序が強要したローカルルールに従っているか」を見ることで確認されることは、所詮、「強要したローカルルールを覚えたかどうか」でしかなく、ローカルルールを覚えること自体が無意味であることから確認も無意味であるように見えます。
kumkum
僕は計算式も一つの文章と理解してます。
6人にペンを8本ずつ渡すには…という問題の場合、答えの単位は「本」になります。なので、8本を6人分という考えになり、8×6=48という計算式になるのですが、8本をどうするかという式なので6の方に単位はありません。
8本 × 6 = 48本
というわけです。
一方6は人数なので、これを先に持ってくると、
6人 × 8 = 48人
となってしまい、人数が増えてしまいます。
なので、式の順番は重要と考えます。
sacla
失礼ながらコメントさせていただきます。
先生が仰られる”6人にペンを8本ずつ渡すには…”という問題の場合
1人あたり8本渡すべきものを6人分用意すと最終的に何本になるかを考えるわけですよね?
そうすると8の方の単位は [本 / 人], 6の方は[人]
以上の議論から
8 [本/ 人] x 6 [人] = 48 [本]
ここで6を先に持ってきて
6 [人] x 8 [本/ 人] = 48 [本]
としても単位は変わることはないと考えております。
したがって, 式の順番はことの本質に関わることではないと考えておりますが如何でしょうか。
iina-kobe
かけ算は足し算の延長線上で教えるものなので、それは無理があります。
物理屋
無理ですか?
そうすると、3[m]×5[m]が15[㎡]にならなくなってしまいますが。
そもそも、式の順番を重要とする立場だからこそ6×8が48[人]になってしまう(あるいは8人に6本ずつになってしまう)のであり、「人数が増えてしまうので順番は重要」というのは因果が逆ですね。
小学校の外の本来の掛け算であれば6×8[本]=48[本]でかまいません。
iina-kobe
よくブログを読んでいただければわかります。あなたもこの方法でかけ算を習ったはずです。かけ算は足し算の延長として習い、その後、交換法則に自ら気付くことで、順番はどっちでもいいんだ!っていうふうに自分で考え、自信をつけ、算数が好きになっていくように指導しております。
物理屋
「社会性のない子」というのは、ある意味、確かにその通りではあるんですが、「授業中に騒ぐな」とか程度ならともかく「本当なら正しいけどバツにする」といったことを理解させるのは低学年に求めるレベルの社会性を超えていると思うんです。無くても仕方ありません。寧ろ、子供に合わせられない先生の方が社会性に問題があると思えます。
一つ分と幾つ分を理解させることに加えて、順序まで幼い子供に教え込むのは、教師にとって大きな労力だと思います。先生から掛け算の説明をする分には一つの考え方だけ伝えれば済むことで問題はありませんが、順序教育では子供に交換法則とその現実の事象における意味を説明した後でももう一方の順序を禁止し続けるのですから。そこで、現場では往々にして「逆順だと本当に間違っている」ということにしてしまい、その理由として「単位のサンドイッチ」が教えられ、一つ分と幾つ分は蔑ろにされてしまうわけです。
わざわざ順序なんて守らせなくても、文章にダミーを含む3つ以上の数を入れたり、掛け算でない問題を織り交ぜたりしたテストをすればいいと思います。それで毎回正しい答えが出せるようなら、数的関係は掴めていると考えていいでしょう。長方形の縦と横に相当する関係を把握するのに、縦と横を区別する必要はありません。理解せずに単位を見てるだけの子を理解してると見做したり、理解してない子と理解してて社会性がないだけの子を混同したりすることもなくなります。
iina-kobe
本文にも書いておりますが、個人的には、順序を逆に書いた子供は、式は× 答えは〇という認識でおります。
順序が必要な理由は簡潔に、
https://www.vissenburg.com/2018/05/25/%E3%81%82%E3%81%99%E3%81%AA%E3%82%8D199%E3%80%80%E3%81%8B%E3%81%91%E3%82%89%E3%82%8C%E3%82%8B%E6%95%B0x%E3%81%8B%E3%81%91%E3%82%8B%E6%95%B0/
に書かれております。
縦と横の関係も、教えるときには、縦にいくつが、横にいくつ分という教え方をします。
最終的に交換法則を教えるのは4年生で、その後も、いくつがいくつぶんという関係を理解しているかどうか?のチェックにのみ、順序を守らせる指導となっています。
あなたの仰る通り、ダミーを含む3つ以上の数を入れたりのチェックも行われています。
頭のいい子は不思議に思うかもしれませんが、頭の悪い子でも理解できるようにとの配慮なので仕方ないのです。
学塾ヴィッセンブルク 塾長 朝倉智義
初めまして。
学塾ヴィッセンブルクの朝倉と申します。
当サイトに飛んでくるリンク元として、こちらのサイトがあったのでやってきました。
私も生物関係の記事を良く書くので、生物関係で引用されたのかと思ったら、まさかの算数でした。
えー。
上のコメントを拝見致しました。
クソ難しい長文は、全部は到底読めませんw
管理人様も大変ですね。
ツイッターはやっていないのですが、アカウントを取ったら是非フォローさせてください。
その時にはよろしくお願いいたします。